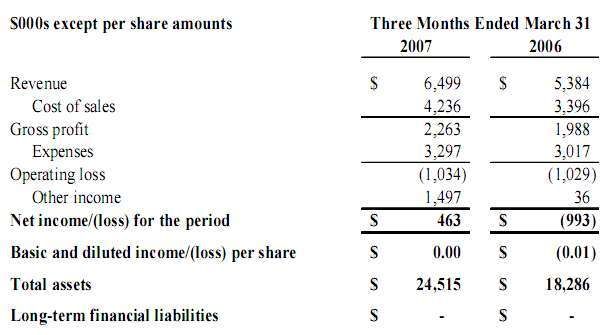
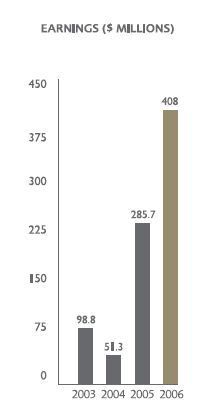
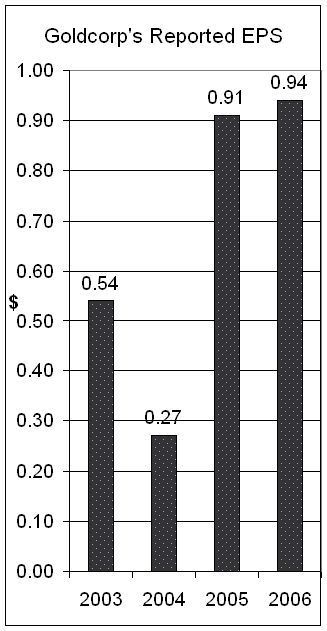
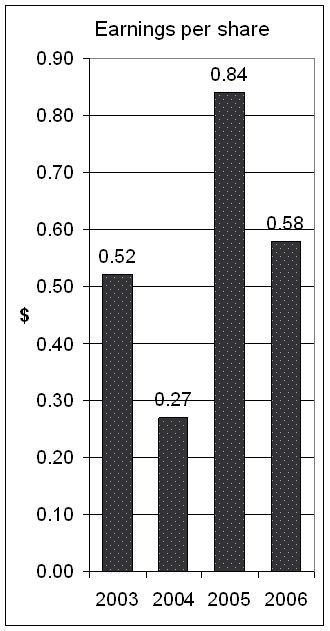
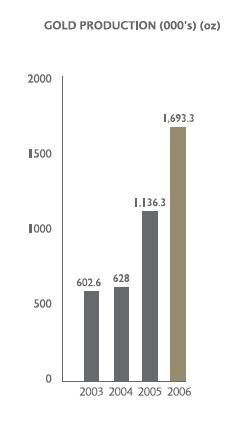
I was 17 when I first got a job as a teller in a credit union in 1979. This is where I first studied mortgages.
Qualifying income was such that no more than 30% of your gross income would be needed to pay the mortgage. Mortgage rates were about 10-12%. You needed qualifying income of $36,345 to qualify for $100,000 of mortgage at 10%. Most mortgages at the time were under $50,000, and people in their 30s were paying off their mortgage on their house, not a condo or a townhouse, but a house with a yard.
The credit unions had technology far ahead of the times and they had a program where I could change the variables in mortgages and view amortization tables, much like you can do today.
The changes intrigued me. I studied how much money a person could save by increasing their payments by relatively small amounts. For example, at 10% the payments on $100,000 mortgage would be about $909 per month over 25 years, and 10% was about what mortgage rates were before they spiked. Increase the payment by 10% and you would have saved 7 years, or 28% of your payments. The table below shows what happens with each 10% increase in payment.
Effects on Amortization Period of increasing payments at a fixed rate of 10%
Example A: $100,000 @ 10%
| Payment | Amort (months)
| Months Reduced (+/- 0.5 months)
| Increase in Payment - (total)
| Decrease in Months to Repay - (total)
| Total Interest Paid
| Interest saved from last 10%*
|
| $908.62 | 300 | N/A
| N/A | N/A | $172,600
| N/A
|
| $999.48 | 216 | 84
| 10% - (10)
| 28% - (28)
| $115,900
| $56,700
|
| $1090.34 | 174 | 42
| 10% - (20)
| 14% - (42)
| $89,700
| $26,200
|
| $1181.21 | 147 | 27
| 10% - (30)
| 9% - (51)
| $73,600
| $16,100
|
| $1272.07 | 128 | 19
| 10% - (40)
| 6.3% - (57.3)
| $62,800
| $10,800
|
$1362.93
| 114
| 14
| 10% - (50)
| 4.7% - (62)
| $55,400
| $7,400
|
$1453.79
| 102.5
| 11.5
| 10% - (60)
| 3.8% - (65.8)
| $49,000
| $6,400
|
$1544.65
| 93.5
| 9
| 10% - (70)
| 3% - (68.8)
| $44,400
| $4,600
|
$1635.52
| 86
| 7.5
| 10% - (80)
| 2.5% - (71.3)
| $40,700
| $3,700
|
$1726.38
| 79.5
| 6.5
| 10% - (90)
| 2.2% - (73.5)
| $37,200
| $3,500
|
$1817.24
| 74
| 5.5
| 10% - (100)
| 1.8% - (75.3)
| $34,500
| $2,700
|
*As number of payments have been averaged to +/- 0.5 of a payment, the error in the total interest can be as much as +/- 0.25 of the payment.
The leverage of how much you could save rapidly declined as you increased payments. Where that first 10% increase brought the number of years from 25 down to 18, increasing by 20% saved an additional 3.5 years, or 14%. By increasing payments by 30%, the number of years to pay back the mortgage was cut by more than half.
Furthermore, the interest saved with that first 10% increase is enormous, 56.7% of the original mortgage amount -- about 1/3rd of the interest overall. And even more amazing, double the payment and you pay only about 1/5th the interest and can pay it off in a little over 6 years.
Effects on Payments of changing interest rates for fixed amortization
Example B: $100,000 over 300 months
| Interest Rate | Change in Interest Rate
| Payment | Increase/ Decrease
| % Change in Payment
|
9%
| -10%
| 839.14
| -69.48
| 7.65%
|
| 9.5% | -5%
| 873.62 | -35.00
| 3.85%
|
| 10% | 0%
| 908.62 | 0
| 0%
|
| 10.5% | 5%
| 944.09 | 35.47
| 3.9%
|
| 11% | 10%
| 980.01 | 71.39
| 7.86%
|
At those interest rates, 0.5% changes did not make huge differences to payments. When 10% is the current mortgage rate, a 1% decline or increase means the interest rate has changed by 10% (change in rate/rate*100%). The relative payment changes by less than the change in the interest rate. Interest rate increases cost more, but are manageable.
If you look at percent of that family income, a 1% increase would cost 2.36% of qualifying income. For most households income would have increased by at least that amount by the time a mortgage needed to be renewed.
Something not shown on the table is that if interest rates went down by 1%, and you kept your payment the same, the amortization would decline to 19.5 years, and you did not give up an ounce of lifestyle. If interest rates cut in half, to 5%, the amortization would decrease to 12.25 years.
The other thing I "played" with was how much would you have to change the payment to reduce amortization by a year at a time?
Effect on Payment of Reducing Amortization Period
Example C: $100,000 @ 10%
| Amort (years) | Monthly Payment ($)
| Increase to reduce 1 year ($)
| Total increase ($)
| % Total increase
| Total Interest Paid ($)
|
| 25 | 908.70 | N/A | N/A | N/A
| 172,610
|
| 24 | 917.39 | 8.69 | 8.69 | 0.96%
| 164,208
|
| 23 | 927.18 | 9.79 | 18.48 | 2.03%
| 155,902
|
| 22 | 938.25 | 11.07 | 29.55 | 3.25%
| 147,697
|
| 21 | 950.78 | 12.53 | 42.08 | 4.63%
| 139,597
|
| 20 | 965.02 | 14.24 | 56.32 | 6.20%
| 131,605
|
| 19 | 981.26 | 16.24 | 72.56 | 7.99%
| 123,727
|
| 18 | 999.84 | 18.58 | 91.14 | 10.0%
| 115,966
|
| 17 | 1021.21 | 21.37 | 112.51 | 12.4%
| 108,327
|
| 16 | 1045.90 | 24.69 | 137.20 | 15.1%
| 100,813
|
| 15 | 1074.61 | 28.71 | 165.91 | 18.3%
| 93,429
|
| 14 | 1108.20 | 33.59 | 199.50 | 22.0%
| 86,178
|
13
| 1147.85
| 39.65
| 239.15
| 26.3%
| 79,064
|
12
| 1195.08
| 47.23
| 286.38
| 31.5%
| 72,091
|
11
| 1251.99
| 56.91
| 343.29
| 37.8%
| 65,262
|
10
| 1321.51
| 69.52
| 412.81
| 45.4%
| 58,581
|
When interest rates were 10% small changes to a family's overall budget to increase mortgage payments brought in enormous financial reward in terms of reducing the number of years to pay back the debt - - it explains how the economic conditions enabled so many people to be paying off their mortgage in their 30s.
For simplicity, $100,000 was used, but when I first started working in the bank few mortgages were over $50,000 and I remember we were shocked when someone applied for and took out a $100,000 mortgage!
I worked in the banks through the period that interest rates doubled. There were two groups of homeowners, those that had gotten into the market recently and those who had been homeowners for a while.
It certainly made things harder for those who had been home owners for a while, but few lost their homes. For most, income had dramatically increased through the 70s, so although it hurt for that renewal period, wages had kept up enough to enable them to keep their homes.
Many who recently bought found themselves over extended and with insufficient income to cover the huge increase in mortgage payment. In Vancouver it was complicated by a housing price bubble. People who bought at the high point lost their homes, their down payments, and in some cases stilled owed money after the home was sold. In retrospect, the lucky ones failed to qualify for a mortgage.
The usurious interest rates were hard, and very, very destructive for some.
Low Interest Destructive?
Low interest rates have been looked at as a good thing for homeowners, but I beg a difference.
No question that if you owned your home, had a mortgage and interest rates decline, you gain, or if you live in a region with emigration. But what happened if you did not own your own home before interest rates declined, live in a region with population growth, and interest rate went down to 4%? First one must compare what changes on low interest rate mortgages look like.
Effects on Amortization Period of increasing payments at a fixed rate of 4%
Example D: $100,000 @ 4%
| Payment | Amort (months)
| Months Reduced (+/- 0.5 months)
| Increase in Payment - (total)
| Decrease in Months to Repay - (total)
| Total Interest Paid
| Interest saved from last 10%
|
| $527.84 | 300 | N/A
| N/A | N/A | $58,351
| N/A
|
| $580.62 | 257 | 43
| 10% - (10)
| 14.3% - (14.3)
| $48,925
| $9,426
|
| $633.41 | 225 | 32
| 10% - (20)
| 10.7% - (25)
| $42,199
| $6726
|
| $686.19 | 200 | 25
| 10% - (30)
| 8.3% - (33.3)
| $37,142
| $5,057
|
| $738.98 | 181 | 19
| 10% - (40)
| 6.3% - (39.7)
| $33,191
| $3,951
|
$791.76
| 165
| 16
| 10% - (50)
| 5.3% - (45)
| $30,016
| $3,175
|
$844.54
| 151
| 14
| 10% - (60)
| 4.7% - (49.7)
| $27,405
| $2,611
|
$897.33
| 140
| 11
| 10% - (70)
| 3.7% - (53.3)
| $25,218
| $2,187
|
$950.11
| 130
| 10
| 10% - (80)
| 3.3% - (56.7)
| $23,360
| $1,858
|
$1002.90
| 122
| 8
| 10% - (90)
| 2.7% - (59.3)
| $21,761
| $1,599
|
$1055.68
| 115
| 7
| 10% - (100)
| 1.3% - (60.7)
| $20,369
| $1,394
|
There is no question that increasing payments reduces the interest to be paid back, but the benefit of increasing that first 10% increase in payment is about half of what it was as a percent in example A, and look at the difference in overall interest savings, $56,700 versus $9,400, about 600% more savings in interest. The leverage of what you can do to improve your economic position by increasing payments and paying is severely compromised when interest rates are low.
Doubling payments resulted in reducing the amortization to 74 months or 6 years and 2 months, but at 4% interest doubling only reduces the amortization to 115 months or 9 years and 7 months. With low interest rates when you double your payment you have to pay for an extra 41 months or 55% longer to pay off the mortgage.
Effects on Payments of changing interest rates for fixed amortization
Example E: $100,000 over 300 months
| Interest Rate | Change in Interest Rate
| Payment | Increase/ Decrease
| % Change in Payment
|
3%
| -25%
| 474.21
| -53.63
| 10.16%
|
| 3.5% | -12.5%
| 500.62 | -27.22
| 5.16%
|
| 4% | 0%
| 527.84 | 0
| 0%
|
| 4.5% | 12.5%
| 555.83 | 27.99
| 5.30%
|
| 5% | 25%
| 584.59 | 56.76
| 10.75%
|
The one percent increase from 4% to 5% results in the payment going up 10.8% when interest rates are low compared to 7.8% when interest rates are higher. Overall, that comes to about 3.24% of qualifying income. It does not sound like a lot, but compared to the 2.36% in example B, the overall relative increase is 37% more.
If interest rates go down to 3% and you keep your payment the same the amortization would decline to 21 years 5 months, 35% less benefit than when when interest rates were higher.
Effect on Payment of Reducing Amortization Period
Example F: $100,000 @ 4%
| Amort (years) | Monthly Payment ($)
| Increase to reduce 1 year ($)
| Total increase ($)
| % Total increase
| Total Interest Paid ($)
|
| 25 | 527.84 | N/A | N/A | N/A
| 58,351
|
| 24 | 540.69 | 12.85
| 12.85
| 2.43%
| 55,719
|
| 23 | 554.75 | 14.06
| 26.91
| 5.10%
| 53,111
|
| 22 | 570.18 | 15.52
| 42.43
| 8.02%
| 50,527
|
| 21 | 587.18 | 16.91
| 59.34
| 11.2%
| 47,969
|
| 20 | 605.98 | 18.80
| 78.14
| 14.8%
| 45,435
|
| 19 | 626.87 | 20.89
| 99.03
| 18.8%
| 42,926
|
| 18 | 650.20 | 23.33
| 122.36
| 23.2%
| 40,443
|
| 17 | 676.39 | 26.19
| 148.55
| 28.1%
| 37,984
|
| 16 | 706.00 | 29.61
| 178.16
| 33.8%
| 35,551
|
| 15 | 739.69 | 33.69
| 211.85
| 40.1%
| 33,144
|
| 14 | 778.35 | 38.66
| 250.51
| 47.5%
| 30,762
|
13
| 823.12
| 44.77
| 295.28
| 55.9%
| 28,406
|
12
| 875.53
| 52.41
| 347.69
| 65.9%
| 26,076
|
11
| 937.67
| 62.14
| 409.83
| 77.6%
| 23,772
|
10
| 1012.45
| 74.78
| 484.61
| 91.8%
| 21,494
|
In the last example, to reduce the amortization period by one year you must increase the payment by 2.43%. Overall, this is an enormous difference in comparison to example C where the payment was increased by 0.96%, relatively speaking about 2.5 times as much.
The big difference is to look at the change for paying back the mortgage in 10 years. In example C if you increase the payment by 45.4% the mortgage is paid off in 10 years, where as when rates are 4% the payment has to be increased by 91.8%.
Enter Housing Costs
On the surface, lower interest rates look like win-win. On $100,000 payments start at 58% of what payments were at 10% interest, and that is an enormous savings. However, the big problem is that in many cities housing costs have increased far beyond the rate of inflation, to the point that people buying are often qualifying for their mortgage with the same parameters as those that first bought when mortgages were 10%.
There are tons of examples that could be used, but I will use what I know. In 1976, after my mother passed away, her two bedroom condo in Kitsilano lay fallow for more than a year for not being able to sell it for about $30k. In that over a year period it ate all of the equity she had built into it as well as the equity of her 3-year-old car. Indeed, when the bank foreclosed on it, her estate owed more than it had. So, $30k for a two bedroom condo in 1977 is what I know to be true.
Today the cheapest two bedroom condo I could find is priced at $379k. This represents an annual rate of return of 8.8% over the past 30 years. Minimum wage at the time was $3/hour. To put it into perspective, if minimum wage had kept up with the increase in housing cost for that period, minimum wage would be about $40/hour, but that's another issue.
To keep things simple, I'll ignore down payments, maintenance fees, property tax, etc. and just do a comparison on the two condo values.
To qualify for 30k at 10% you would have needed about $11,000 of income, or a wage of $5.64/hour. Monthly payments would be $272.61. Total amount paid would be $81,783. Interest is 63.3% of the repayment amount.
To qualify for 379k at 4% you would need $80,000 of income, or a wage of $41.03. Monthly payments would be $2,000.50. Total amount paid would be $600,150. Interest is 36.8% of the total.
On a side note, something that is utterly amazing about this to me is in 1977, as a 15-year-old, I worked part-time as a waitress and with tips I was making about $6/hour. I wonder how many 15-year-olds today could get a part-time job that would pay them $40-45/hour? In light of this enormous economic difference, no wonder so many 30 something year olds were able to pay off their mortgage!
Principal must be repaid, interest repayment is flexible
Ignoring the gross decline in wages relative to housing costs, a serious difference in the two examples is the amount of interest in the payments. By comparison, today's new buyer is grossly under privileged in their ability to get ahead by accelerating payments because the majority of the amount to be repaid is principal. When the majority was interest, that repayment could be drastically reduced by modest compromises in lifestyle.
I would further suggest that had interest rates remained higher, housing prices would be lower because less people would qualify for mortgages, and housing prices are determined by supply and demand.
So had interest rates only declined to 7% that 35-year-old $379,000 condo might be for sale for $283,000, a price that would also require $80,000 of income if interest rates were 7%, only in this case 53% would be interest. The increase in the price of the condo would still be way ahead of inflation at 7.7% per year.
If interest rates had remain in the 10% range one would only qualify for $221,000 with $80,000 of income and 63.3% of the repayment would be interest, and rate of increase in the price of the condo would be 6.9%.
Low interests rates have enabled housing prices to increase beyond reasonable levels and drastically reduced a new home owner's ability to reduce their repayment burden as most of the amount to repay is now principal.
Low interest is a function of inflation
Probably the most important disabling point for newer buyers is that low interest rates are a function of inflation. Low interest rates mean inflation is lower, which means wage increases are lower. When interest rates were high home owners could count on wage increases of 5-8% and the housing burden in their budget rapidly declined, enabling them to make far more discretionary income decisions. With low interest rates inflation is low and wage go up slowly. Indeed, many workers have experienced years with no wage increase. Increasing repayment of mortgage debt is not so easy when wages remain relatively flat.
So, Are Low Interest Rates as Destructive as Usury?
The usurious interest rates cost most people a couple hard years. Newer buyers will have a lifetime of hard years repaying their mortgages because flat wages disables them from being able to increase payments very much, if at all, and since most of the repayment amount is principal there is little power to improve financial position from leverage of increased payments. Furthermore, it isn't likely that new home owners will enjoy wealth creating due to appreciation of their home values. They have significant downside risk.
Very few who had been a home owner over 3 years lost their home from usurious interest rates of the early 80s. Housing prices doubled from the late 70s to the early 80s and it was the ones who paid the high prices who lost their homes and were left with massive debt to repay, the rest had to tighten their belts and deal with loss of lifestyle.
So, it depends on who you ask. There is no question they were a boom for people in the housing market early and that today's buyers will never enjoy the wealth creation it gave to generations before.
Read More......
![[Most Recent Quotes from www.kitco.com]](http://www.kitconet.com/charts/metals/base/spot-copper-60d.gif)
![[Most Recent Quotes from www.kitco.com]](http://www.kitconet.com/charts/metals/base/lme-warehouse-copper-60d.gif)
![[Most Recent Quotes from www.kitco.com]](http://www.kitconet.com/charts/metals/base/spot-zinc-60d.gif)
![[Most Recent Quotes from www.kitco.com]](http://www.kitconet.com/charts/metals/base/lme-warehouse-zinc-60d.gif)